Assistente em Administração - 2014

Beatriz tem um cartão verde, um cartão vermelho e um cartão azul. Em cada cartão, há exatamente um número (10, 20 ou 30) e uma letra (X, Y ou Z). São feitas as seguintes afirmações sobre esses cartões: - O número no cartão verde é menor que o do cartão vermelho, o qual é menor que o do cartão azul. - Y e 20 estão no mesmo cartão. - X e 10 não estão no mesmo cartão. Nessas condições, é verdade que

Quintino possui um bode que sempre espirra antes de uma chuva. O bode de Quintino espirrou hoje. Isso significa que

No quadro abaixo, cada letra X deve ser substituída por um número do conjunto {1, 2, 3, 4}, de modo que não apareçam números iguais em uma mesma linha nem em uma mesma coluna.

Ao final da correta substituição, teremos que a soma dos números nos quadros sombreados é

Sabendo-se que todos os riláceos são polibas, que nenhum poliba é ceteu e que todos os ceteus são altarves, é correto concluir-se que

Em Pamonholândia, há dois tipos de pessoas: as que sempre mentem e as que sempre falam a verdade. Em um ano de eleições, três candidatos A, B e C, afirmaram: – Candidato A: “o candidato B é mentiroso”. – Candidato B: “o candidato C é mentiroso”. – Candidato C: “A é mentiroso ou B é mentiroso”. É correto afirmar-se que

Inicialmente, havia dez lâmpadas, cada uma com um interruptor próprio. Ao acionar o interruptor de uma lâmpada, seu estado muda de acesa para apagada e vice-versa. Estando todas as dez lâmpadas apagadas, João acionou sete interruptores. Logo em seguida, Pedro acionou seis interruptores. Ao final das interferências de Pedro, há, certamente,

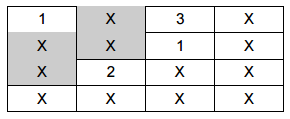
Para cada número natural n considere um quadrado de lado n dividido em n² quadradinhos de lado 1. Pintam-se os quadradinhos de branco e preto, de modo que quadradinhos com um lado em comum tenham cores distintas. A figura abaixo representa uma possibilidade no caso n = 4. Seja b o número de quadradinhos brancos e p o número de quadradinhos pretos no interior do quadrado de lado n. É correto afirmar-se que

O conjunto P é formado por pares ordenados de números reais positivos. Sobre este conjunto, sabe-se que - (1, 1) ∈ P; - Se (a, b) ∈ P, então (a + 1, b + 2) ∈ P. Sobre o conjunto P, é possível afirmar-se que

Uma sequência do tipo ABCD indica que o procedimento A é realizado primeiro, depois o procedimento B, depois o C e, por fim, o D. Duas sequências de procedimentos são equivalentes, quando, agindo sobre o mesmo número não nulo, fornecem resultados iguais. Considere as seguintes sequências: (1) JKJK (2) JJKK (3) JKKJ (4) KJKJ Se o procedimento J inverte o número e o procedimento K dobra o número, então são equivalentes as sequências

Um caixa eletrônico dispõe apenas de notas de 2 reais e 5 reais. Sobre saques nesse caixa, é correto afirmar-se que