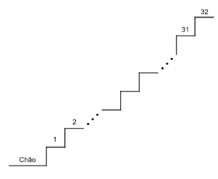
Oficial Bombeiro Militar - 2023
Beatriz estava na escadaria de seu prédio, que tem 32 degraus, numerados conforme a figura ao lado. Ela, primeiramente, desceu 6 degraus e depois subiu 12 degraus, percebendo que ainda faltavam 5 degraus para chegar no topo da escadaria. Em que degrau ela estava inicialmente?
Ana quer descobrir a senha do celular de seu irmão Carlos, a qual é formada por uma sequência de quatro dígitos numéricos dentre 0, 1, 2, 3, 4, 5, 6, 7, 8 e 9. Ela sabe que o irmão sempre usa, em suas senhas, os três dígitos de sua residência: 4, 6 e 8. Recentemente, ela descobriu que o número formado pela senha é ímpar. De acordo com essas informações, quantas possibilidades Ana deve considerar para descobrir a senha de Carlos?
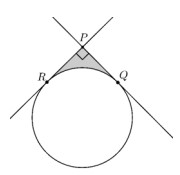
Duas retas no plano se intersectam no ponto P , formando um ângulo reto. Além disso, essas retas são tangentes a uma circunferência nos pontos Q e R , conforme ilustra a figura ao lado. Sabendo que o perímetro da região hachurada mede (2 π + 8) cm, assinale a alternativa que corresponde à medida do raio da circunferência em cm.
Sejam p(x) = x + a e q(x) = x2 - b funções, com a e b números reais. Sabendo que r = 1/2 é a única raiz da função composta f(x) = q(p(x)) , assinale a alternativa que corresponde à soma a + b .
Sabendo que sen(2x) = 3/5, assinale a alternativa que corresponde ao valor de [ sen(x) + cos(x) ]2.
Considere a função f(x) = x 2 + 6x - 8 . No plano cartesiano, sejam P e Q as intersecções do gráfico de f com o eixo x . Sendo R = (a,b) um ponto do gráfico de f , com b>0 , assinale a alternativa que corresponde ao maior valor numérico possível da área do triângulo PQR .
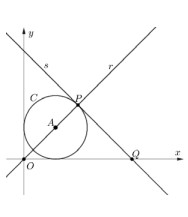
A circunferência C na figura ao lado está centrada no ponto A = (1,1) e tangencia os eixos coordenados. A reta r passa pela origem 0 e pelo ponto A , intersectando a circunferência no ponto P , conforme indica a figura. A reta s é tangente à circunferência no ponto P e intersecta o eixo x no ponto Q . Assinale a alternativa que corresponde à abcissa do ponto Q .
Um bolo é retirado do forno e começa a resfriar segundo a expressão T(t) = 30 + 150 a -0,05 t , com a >1, sendo T a temperatura do bolo e t o tempo decorrido em minutos. Assinale a alternativa que corresponde ao tempo em que o bolo atingirá a metade da temperatura inicial que apresentava quando foi retirado do forno em t = 0. (Use se necessário loga 2 = 0,7 e loga 5 = 1,6).
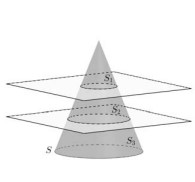
Um cone circular reto S é dividido por dois planos paralelos à sua base, formando três sólidos S 1, S 2 e S 3, conforme a figura ao lado. Os volumes de S 1, S2 e S 3, nessa ordem, estão em progressão geométrica com razão q > 1. O quociente entre o raio do cone S e o raio do cone menor S 1 é igual a 3√7 . Assinale a alternativa que corresponde à razão q .
O texto a seguir é referência para a questão.
Em todas as questões, as medições são feitas por um referencial inercial. O módulo da aceleração gravitacional é representado por g. Onde for necessário, use g = 10 m/s2 para o módulo da aceleração gravitacional.
Capacitores são elementos de circuito que podem armazenar energia quando submetidos a uma diferença de potencial. Num dado circuito, deseja-se que um capacitor de capacitância C armazene uma energia U = 8,0 mJ quando submetido a uma diferença de potencial Δ V = 4,0 V entre seus terminais. Considerando as informações apresentadas, assinale a alternativa que apresenta corretamente o valor da capacitância C desse capacitor.