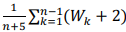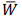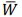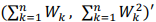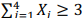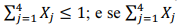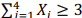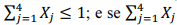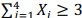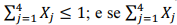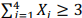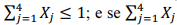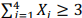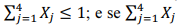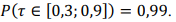Analista Judiciário – Área: Apoio Especializado – Especialidade: Estatística - 2024
Uma amostra aleatória simples de tamanho n > 1 é retirada de uma distribuição exponencial com média µ; tal amostra é representada pelo conjunto {W1,…, Wn} constituído por n variáveis aleatórias independentes e identicamente distribuídas.
Tendo como referência as informações precedentes, julgue o próximo item.
Um estimador consistente da média µ é
.
Uma amostra aleatória simples de tamanho n > 1 é retirada de uma distribuição exponencial com média µ; tal amostra é representada pelo conjunto {W1,…, Wn} constituído por n variáveis aleatórias independentes e identicamente distribuídas.
Tendo como referência as informações precedentes, julgue o próximo item.
Se
denota a média amostral, então o estimador de máxima verossimilhança para a mediana populacional é
× ln(2).
Uma amostra aleatória simples de tamanho n > 1 é retirada de uma distribuição exponencial com média µ; tal amostra é representada pelo conjunto {W1,…, Wn} constituído por n variáveis aleatórias independentes e identicamente distribuídas.
Tendo como referência as informações precedentes, julgue o próximo item.
O vetor
representa uma estatística conjuntamente suficiente para a estimação da média µ e da variância populacional.
Uma amostra aleatória simples de tamanho n > 1 é retirada de uma distribuição exponencial com média µ; tal amostra é representada pelo conjunto {W1,…, Wn} constituído por n variáveis aleatórias independentes e identicamente distribuídas.
Tendo como referência as informações precedentes, julgue o próximo item.
A moda amostral é um estimador para a média µ.
Uma amostra aleatória simples X1, X2, X3, X4 será retirada de uma população Bernoulli para testar a hipótese nula H0: p = 0,2 contra a hipótese alternativa H1: p = 0,4, em que p denota a probabilidade de sucesso de um ensaio de Bernoulli. A hipótese H0 será rejeitada se
; H0 não será rejeitada se
= 2, a hipótese nula será rejeitada com probabilidade y.
Com base nessas informações, julgue o item seguinte.
Comparativamente a outros testes de mesmo tamanho, o teste em tela é considerado uniformemente mais poderoso.
Uma amostra aleatória simples X1, X2, X3, X4 será retirada de uma população Bernoulli para testar a hipótese nula H0: p = 0,2 contra a hipótese alternativa H1: p = 0,4, em que p denota a probabilidade de sucesso de um ensaio de Bernoulli. A hipótese H0 será rejeitada se
; H0 não será rejeitada se
= 2, a hipótese nula será rejeitada com probabilidade y.
Com base nessas informações, julgue o item seguinte.
Para que o tamanho do teste aleatorizado seja igual a 5%, o valor da probabilidade y deverá ser igual a 0,1484375.
Uma amostra aleatória simples X1, X2, X3, X4 será retirada de uma população Bernoulli para testar a hipótese nula H0: p = 0,2 contra a hipótese alternativa H1: p = 0,4, em que p denota a probabilidade de sucesso de um ensaio de Bernoulli. A hipótese H0 será rejeitada se
; H0 não será rejeitada se
= 2, a hipótese nula será rejeitada com probabilidade y.
Com base nessas informações, julgue o item seguinte.
Se o resultado da amostragem for 0, 0, 1, 0, o nível descritivo do teste será igual a 0,4096.
Uma amostra aleatória simples X1, X2, X3, X4 será retirada de uma população Bernoulli para testar a hipótese nula H0: p = 0,2 contra a hipótese alternativa H1: p = 0,4, em que p denota a probabilidade de sucesso de um ensaio de Bernoulli. A hipótese H0 será rejeitada se
; H0 não será rejeitada se
= 2, a hipótese nula será rejeitada com probabilidade y.
Com base nessas informações, julgue o item seguinte.
Se a hipótese alternativa for modificada para H1: p = 0,6, mantendo-se a mesma hipótese nula e o mesmo tamanho do teste aleatorizado, então a regra de decisão proposta não sofrerá modificações.
Uma amostra aleatória simples X1, X2, X3, X4 será retirada de uma população Bernoulli para testar a hipótese nula H0: p = 0,2 contra a hipótese alternativa H1: p = 0,4, em que p denota a probabilidade de sucesso de um ensaio de Bernoulli. A hipótese H0 será rejeitada se
; H0 não será rejeitada se
= 2, a hipótese nula será rejeitada com probabilidade y.
Com base nessas informações, julgue o item seguinte.
Se y = 0, o poder do teste será inferior a 20%.
Julgue o item a seguir, considerando que Tn = T (X1,…, Xn) seja um estimador viciado para o parâmetro desconhecido τ de uma população X, no qual X1,…, Xn representa uma amostra aleatória simples de tamanho n, e denotando sua variância como D2 = Var[Tn].
Se [0,3; 0,9] representa o intervalo de 99% de confiança para τ, então