Perito Criminal - 2013

O Sr. João é um economista aposentado que resolveu melhorar sua qualidade de vida comprando uma pousada com 40 suítes em uma bela região praiana. Com base em dados do proprietário anterior, ele deduziu duas funções para gerenciar seu negócio: a função do preço (p) por diária da suíte (x) e a da receita (R). As funções foram definidas, respectivamente, por: p( x ) = - 5x + 350 e R ( x ) = - 5x2 + 350 x.

Considerando essas funções, o preço que o Sr. João deve cobrar para maximizar a receita é

Uma entidade filantrópica fez um levantamento dos serviços prestados em certa região e observou que 1.680 famílias foram atendidas por uma equipe de 12 funcionários em 5 dias de trabalho de 8 horas por dia. Elaborou um novo planejamento logístico em que as equipes seriam formadas por 5 funcionários que iriam trabalhar 6 dias de 4 horas por dia. Nesse novo planejamento, o número de famílias que serão atendidas por equipe será igual a

Uma companhia aérea decidiu solicitar a uma empresa especializada kits contendo uma mistura de sementes oleaginosas para ofertar aos seus clientes. Os kits deveriam conter 100 g de uma mistura de amendoim, amêndoa e avelã. A companhia aérea solicitou que a quantidade de amêndoa fosse igual a um terço da soma das outras duas e informou que estava disposta a pagar R$ 1,15 por kit. A empresa especializada sabe que o quilo do amendoim custa R$ 5,00, o de amêndoa, R$ 20,00 e o de avelã, R$ 16,00. A quantidade, em gramas, de cada semente que a empresa deve colocar em cada kit, de tal maneira que atenda a todas as exigências estabelecidas pela companhia aérea, deverá ser, respectivamente, de:

Um artista recebeu uma encomenda para fazer um painel, esculpindo em uma chapa de aço folhas e flores. Para determinar o formato do painel, o artista considerou a chapa de aço como um plano cartesiano cujos eixos a dividiram em quatro quadrantes. Utilizou um segmento de reta e o deslocou nesse plano cartesiano, de tal forma que uma das extremidades permanecia sempre no eixo y e o seu ponto médio permanecia sempre no eixo x. Dessa maneira, o formato da figura desenhada pela outra extremidade é uma

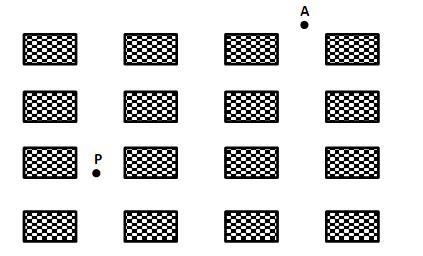
Um policial faz sua ronda em uma região formada por 16 quarteirões dispostos segundo a figura abaixo. Ele encontrava-se exatamente no ponto P quando recebeu um aviso pelo rádio informando sobre um assaltante localizado no ponto A. O policial dirige-se ao local em que se encontra o assaltante pelo caminho mais curto, isto é, movendo-se da esquerda para a direita e de baixo para cima.

Nessas condições, o número de caminhos diferentes que o policial poderá fazer é:

Uma empreiteira está construindo um parque e o paisagista determinou que, ao longo de uma das ruas retilíneas, serão plantadas 60 palmeiras imperiais com distância de 1 metro entre uma e outra, cujas covas já estão preparadas. O funcionário responsável pelo plantio, colocação das palmeiras nas covas previamente preparadas, recebe as mudas de uma plataforma situada a uma distância de 15 metros da primeira palmeira plantada e, a cada viagem, consegue carregar somente 3 palmeiras. Começando e terminando na plataforma, o percurso total, em metros, que ele terá que caminhar até colocar todas as palmeiras em suas respectivas covas será igual a

Uma pesquisa sobre acidentes em rodovias observou que, de todos os acidentes fatais, 24% envolveram capotagens e 15,8%, carros utilitários. Considerando que uma capotagem não tenha sido envolvida, 5,6% de todos os acidentes fatais envolveram carros utilitários. Sabendo-se que o acidente fatal envolveu um carro utilitário, a probabilidade de que ele tenha sido capotagem é de, aproximadamente,

Duas sequências são formadas pelos termos gerais:

. Quando n tende para o infinito, pode-se observar que o comportamento dessas sequências é dado, respectivamente, por:

Com o objetivo de diversificar sua renda, um produtor rural decidiu construir um tanque para criar tilápias. Colocou, inicialmente, 1.000 tilápias e, descuidadamente, deixou cair também 8 piabas. Suponha que o aumento das populações de piabas e tilápias ocorre segundo as leis P(t)=P010t e T(t)=T02t , respectivamente, em que P0 é a população inicial de piabas, T0 é a população inicial de tilápias e t o número de anos contados a partir do ano inicial. O tempo, em anos, em que o número de piabas será igual ao número de tilápias é

Um laboratório está testando um tipo de isca para formigas. A isca tem o formato de uma circunferência e foi fixada numa bancada experimental, quadriculada por um plano cartesiano, com centro em (0, -2). Uma formiga tangenciou a isca no ponto (1, 2).

A equação da reta tangente à circunferência nesse ponto é dada por: