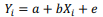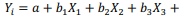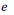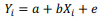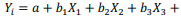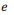Economista - 2022
Com base nos modelos de regressão linear simples (equação 1) e de regressão linear múltipla (equação 2), julgue o item a seguir. A homocedasticidade, conceito que implica que o erro não-observável “e” de uma regressão múltipla seja constante, é uma das condições para que os coeficientes b 1, b 2 e b 3 da equação 2 sejam não-viesados e consistentes.
Considerando a microeconomia, julgue o item a seguir, conforme as condições e hipóteses apresentadas em cada item. Para uma função utilidade do tipo U ( x,y ) = ( x+y )1/2, em que x e y são as quantidades consumidas de cada um dos dois bens disponíveis na economia, a taxa marginal de substituição entre os bens x e y é alterada por transformações monotônicas na função utilidade.
Considerando a microeconomia, julgue o item a seguir, conforme as condições e hipóteses apresentadas em cada item. Caso a função utilidade de um consumidor seja dada por U ( x,y ) = x 1/2 + y , em que x e y são as quantidades consumidas de cada um dos dois bens disponíveis na economia, o efeito-renda da demanda por x será nulo.
Considerando a microeconomia, julgue o item a seguir, conforme as condições e hipóteses apresentadas em cada item. Considerando uma economia com apenas duas firmas que produzem o mesmo produto q e que possuem custo marginal de produção igual a 50, suponha que a demanda pelo produto q nessa economia seja dada pela função P = 300 - q /4, em que P é o preço do produto e q é a quantidade consumida do produto. Nesse contexto, se q 1 é a quantidade produzida do produto q pela firma 1 e q 2 é a quantidade produzida do produto q pela firma 2, no equilíbrio de Cournot, o preço será igual a P = 300 - 1000/12.
Considerando a microeconomia, julgue o item a seguir, conforme as condições e hipóteses apresentadas em cada item.
Considere que uma empresa possua uma função de produção Cobb-Douglas dada por 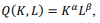 em que K e L representam, respectivamente, as quantidades de capital e trabalho necessárias para a produção do produto Q , sendo α e β constantes positivas. Nesse caso, a elasticidade de escala é igual a α + β.
em que K e L representam, respectivamente, as quantidades de capital e trabalho necessárias para a produção do produto Q , sendo α e β constantes positivas. Nesse caso, a elasticidade de escala é igual a α + β.
Considerando a microeconomia, julgue o item a seguir, conforme as condições e hipóteses apresentadas em cada item. Suponha que um indivíduo consuma apenas dois bens, sendo o primeiro um bem normal e o segundo, um bem inferior. Nessa situação, caso haja um aumento de preço do bem normal, o consumo do bem inferior aumentará em decorrência do efeito-renda.
Considerando a microeconomia, julgue o item a seguir, conforme as condições e hipóteses apresentadas em cada item. Considerando-se que a função de custo total de uma firma seja dada por CT = 2 x 3 - 180 x 2 + 7200 x + 540, em que x é a quantidade produzida do produto, é correto afirmar que, nesse caso, o estágio racional de produção se inicia para um nível de produto igual a 15 unidades.
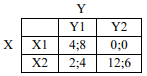
Os jogadores X e Y disputam um jogo estático, cada qual com duas estratégias possíveis: X1 ou X2 para o jogador X; e Y1 ou Y2 para o jogador Y. Ambos devem escolher simultaneamente uma de suas possíveis estratégias, considerando os ganhos apresentados na tabela a seguir, na qual os ganhos do jogador X são apresentados à esquerda e os ganhos do jogador Y são apresentados à direita.
Assim, se o jogador X adotar a estratégia X1 e o jogador Y adotar a estratégia Y1, o jogador X ganhará 4 reais e o jogador Y ganhará 8 reais.
Com base nessas informações, julgue o item a seguir. O jogo não possui equilíbrio em estratégias dominantes.
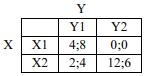
Os jogadores X e Y disputam um jogo estático, cada qual com duas estratégias possíveis: X1 ou X2 para o jogador X; e Y1 ou Y2 para o jogador Y. Ambos devem escolher simultaneamente uma de suas possíveis estratégias, considerando os ganhos apresentados na tabela a seguir, na qual os ganhos do jogador X são apresentados à esquerda e os ganhos do jogador Y são apresentados à direita.
Assim, se o jogador X adotar a estratégia X1 e o jogador Y adotar a estratégia Y1, o jogador X ganhará 4 reais e o jogador Y ganhará 8 reais.
Com base nessas informações, julgue o item a seguir. O par de estratégias (X1;Y1) é um equilíbrio de Nash em estratégias puras.