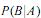Agente Administrativo - 2012
Com base nessas informações, julgue os itens de 106 a 111.
A quantidade de pessoas do sexo masculino e do sexo feminino que trabalha nos referidos postos de combustível e que apresenta concentrações de chumbo no sangue inferiores a 5 µg·dL-1 é igual ou menor que 50 e 25, respectivamente.
Considere os eventos A, B, C e D, definidos abaixo, relativos ao
número de veículos por família em determinada cidade.
A = uma família possui 1 ou mais veículos;
B = uma família possui 2 ou mais veículos;
C = uma família possui 3 ou mais veículos;
D = uma família possui 4 ou mais veículos.
Considere, ainda, que as probabilidades de ocorrência desses
eventos são: P(A) = 0,9; P(B) = 0,6; P(C) = 0,3 e P(D) = 0. Com
base nessas informações, julgue os itens que se seguem.
A probabilidade de uma família na referida cidade possuir exatamente 1 veículo é igual a 0,3.
Considere os eventos A, B, C e D, definidos abaixo, relativos ao
número de veículos por família em determinada cidade.
A = uma família possui 1 ou mais veículos;
B = uma família possui 2 ou mais veículos;
C = uma família possui 3 ou mais veículos;
D = uma família possui 4 ou mais veículos.
Considere, ainda, que as probabilidades de ocorrência desses
eventos são: P(A) = 0,9; P(B) = 0,6; P(C) = 0,3 e P(D) = 0. Com
base nessas informações, julgue os itens que se seguem.
A probabilidade de uma família na referida cidade não possuir veículo é igual ou superior a 0,15.
Considere os eventos A, B, C e D, definidos abaixo, relativos ao
número de veículos por família em determinada cidade.
A = uma família possui 1 ou mais veículos;
B = uma família possui 2 ou mais veículos;
C = uma família possui 3 ou mais veículos;
D = uma família possui 4 ou mais veículos.
Considere, ainda, que as probabilidades de ocorrência desses
eventos são: P(A) = 0,9; P(B) = 0,6; P(C) = 0,3 e P(D) = 0. Com
base nessas informações, julgue os itens que se seguem.
O número médio de veículos por família na referida cidade é igual ou superior a 2.
Considere os eventos A, B, C e D, definidos abaixo, relativos ao
número de veículos por família em determinada cidade.
A = uma família possui 1 ou mais veículos;
B = uma família possui 2 ou mais veículos;
C = uma família possui 3 ou mais veículos;
D = uma família possui 4 ou mais veículos.
Considere, ainda, que as probabilidades de ocorrência desses
eventos são: P(A) = 0,9; P(B) = 0,6; P(C) = 0,3 e P(D) = 0. Com
base nessas informações, julgue os itens que se seguem.
A probabilidade condicional
é inferior a 0,6.
Considere os eventos A, B, C e D, definidos abaixo, relativos ao
número de veículos por família em determinada cidade.
A = uma família possui 1 ou mais veículos;
B = uma família possui 2 ou mais veículos;
C = uma família possui 3 ou mais veículos;
D = uma família possui 4 ou mais veículos.
Considere, ainda, que as probabilidades de ocorrência desses
eventos são: P(A) = 0,9; P(B) = 0,6; P(C) = 0,3 e P(D) = 0. Com
base nessas informações, julgue os itens que se seguem.
Os eventos A e D são independentes.
A tabela acima apresenta as estatísticas produzidas em um
levantamento acerca do número diário de acidentes que envolvem
motocicletas em determinado local. Com base nessas informações,
julgue os próximos itens.
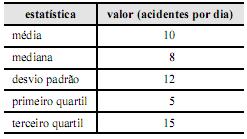
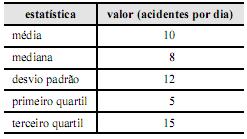
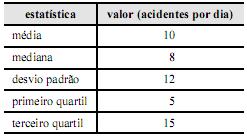
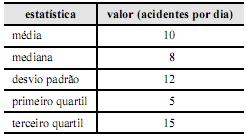
É correto inferir que a probabilidade de haver, em determinado dia, 10 ou mais acidentes que envolvam motocicletas no referido local é estritamente inferior a 0,5.
A tabela acima apresenta as estatísticas produzidas em um
levantamento acerca do número diário de acidentes que envolvem
motocicletas em determinado local. Com base nessas informações,
julgue os próximos itens.
O coeficiente de variação da distribuição em questão é superior a 1 e inferior a 1,4.
A tabela acima apresenta as estatísticas produzidas em um
levantamento acerca do número diário de acidentes que envolvem
motocicletas em determinado local. Com base nessas informações,
julgue os próximos itens.
Segundo o coeficiente de assimetria de Pearson, a distribuição desse número diário de acidentes apresenta assimetria negativa.
A tabela acima apresenta as estatísticas produzidas em um
levantamento acerca do número diário de acidentes que envolvem
motocicletas em determinado local. Com base nessas informações,
julgue os próximos itens.
A variância da distribuição do número diário de acidentes com motocicletas no referido local é inferior a 100.